CourseraのMachine Learningから線形回帰を学んだのでまとめてみた

CourseraのMachine Learningを受講しています。時間を見つけてはコツコツ進めて今のところWeek4に差し掛かったところです。Week4ではNeural Networksの話に入り一段とレベルが高くなった印象を受けています。Week1からWeek3までに学んだことを復習する必要があるなと焦りが生まれました。

受講中は配布される資料や動画を見たり他の日本人の方のブログを拝見したりと課題に取り組んできました。このタイミングで復習して整理することでWeek4以降の学習が快適になるのではないかと淡い期待を込めてWeek1からまとめてみます。

Machine Learning - Stanford University | Coursera

こちらが受講しているMachine Learningのコースです。MOOCは好きな時間に進められるし前編英語（動画は日本語字幕あり）なので英語の学習になってオススメです。

Machine Learning - Stanford University | Coursera

どこまでの内容をまとめるか

このエントリではWeek1の内容に触れています。

線形回帰とは？

ある土地の家の価格とその家の部屋数の相関をグラフで表すと以下のようになったとします。

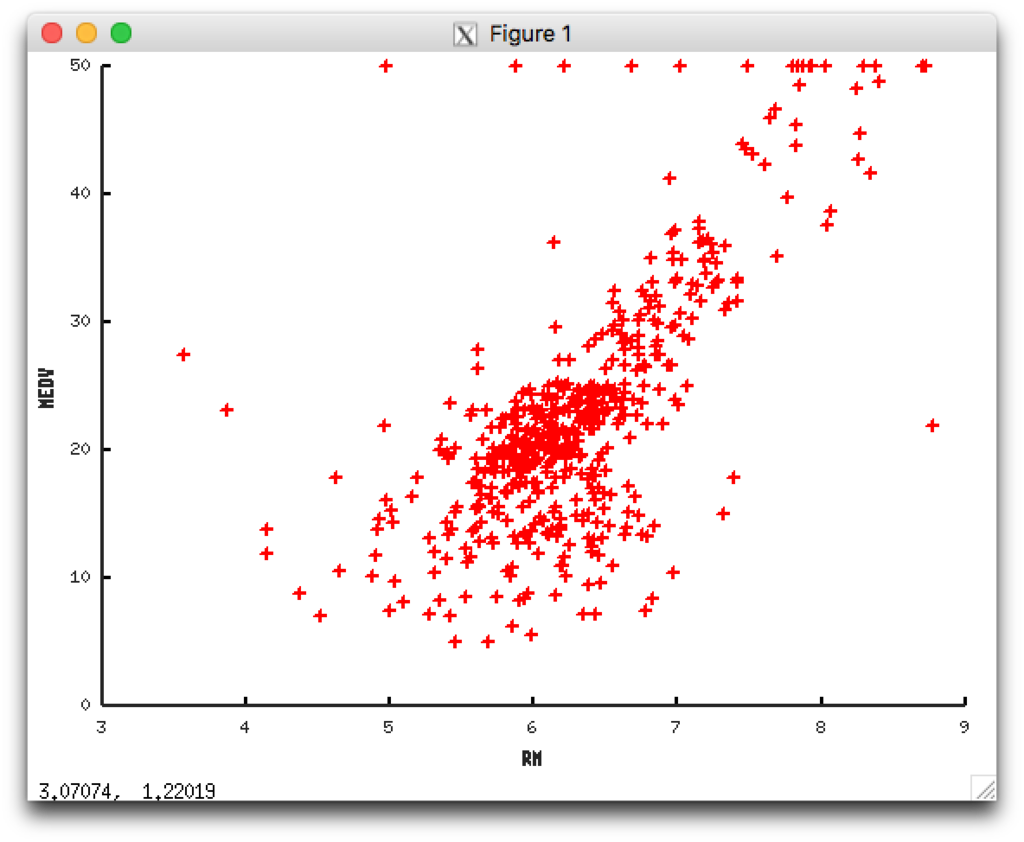
Xが部屋数（RM）でYが価格（MEDV）です。

（出典：Housing Data Set）

※ このデータは部屋数以外に、その土地の犯罪率だったり児童と教師の比率など複数の要素から構成されています。

部屋数が4つの場合や部屋数が7つの場合はグラフから予想できそうです。 このとき頭の中ではグラフに右肩上がりな直線をイメージして予想できますが、この直線を数式から導き出すことを学びました。 この導き方は統計学では回帰分析の一種として線形回帰と呼ばれています。

仮定関数と目的関数

部屋数をX、部屋の価格をYとすると相関を表すグラフを引くための1次関数の式は次のようになります。（懐かしい数式）

\displaystyle Y = aX + b

Machine Learningのコースではθをつかって次のような式で定義しています。

\displaystyle h_\theta (X) = \theta_0 + \theta_1(X)

h_\theta (X) は仮定関数と呼ばれます。家の価格予想に最適な直線を引くために \theta_0 と \theta_1の数値を変えながらグラフにフィットした仮定関数を導き出します。 つまり右肩上がりの直線のグラフを引くために最適な aX + b の aとbを決めるということですね。

仮定関数がフィットしているか計算するための関数である目的関数があります。

{ \displaystyle J(\theta_0, \theta_1) = \frac{1}{2m}\sum_{i=1}^{m} (h_\theta (X_i) - Y_i)^2 }

この目的関数をつかって J(\theta_0, \theta_1)を最小にする \theta_0 と \theta_1を導き出します。

最急降下法

目的関数を最小にする方法に最急降下法があります。

{ \displaystyle \theta_j = \theta_j - \alpha \sum_{i=1}^{m} (h_\theta (x^{(i)}) - y^{(i)}) x_j\ ^{(i)} }

ここで微分が出てきます。微分は傾きを求めますがこのアルゴリズムを使い傾きが最小になるまで学習を繰り返していきます。傾きの値が最小になるほどグラフにフィットした \theta_jが求められます。 \alphaは学習率と呼ばれ数値が大きいほど傾きの変動幅が大きくなりフィットしたデータが得られず、小さいほど学習はゆっくりと進み確実にデータにフィットした値が求められます。

Octaveでプログラム化する

コースの課題ではOctaveを使いプログラミング課題を提出します。 最初に示した家の価格と部屋数のグラフのデータを使い、更にこれまでのアルゴリズムからデータにフィットした直線をグラフにプロットしてみます。

目的関数

1
2
3
4

function J = computeCost(X, y, theta)
    m = length(y);
    J = sum((X*theta -y).^2) / (2* m);
end

最急降下法

1
2
3
4
5
6
7
8
9

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
    m = length(y);
    J_history = zeros(num_iters, 1);

    for iter = 1:num_iters
        theta = theta - alpha / m * X' * (X * theta -y);
        J_history(iter) = computeCost(X, y, theta);
    end
end

目的関数を求めグラフにプロットする。そして部屋数が5つのときの価格を予想する。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

%% Initialization
clear ; close all; clc
data = load("housing.txt");
x = data(:, 6);
y = data(:, 14);
m = length(y);

theta = zeros(2, 1);
X = [ones(m, 1), x]

%% Compute Cost
J = computeCost(X, y, theta)

%% Gradient Descent
iterations = 1500;
alpha = 0.01;
[theta J_history] = gradientDescent(X, y, theta, alpha, iterations);

%% Output
fprintf('Initial cost = %f\n', J);
fprintf('Final cost = %f\n', J_history(iterations));
fprintf('Theta found by gradient descent: ');
fprintf('%f %f \n', theta(1), theta(2));

%% Plot data
figure; hold on;
plot(x, y, 'r+', 'LineWidth', 2);
plot(X(:,2), X*theta, '-')
xlabel('RM');
ylabel('MEDV');

%% Predict
fprintf('for RM = 5, MEDV = %f\n', [1, 5] *theta);

出力したグラフ

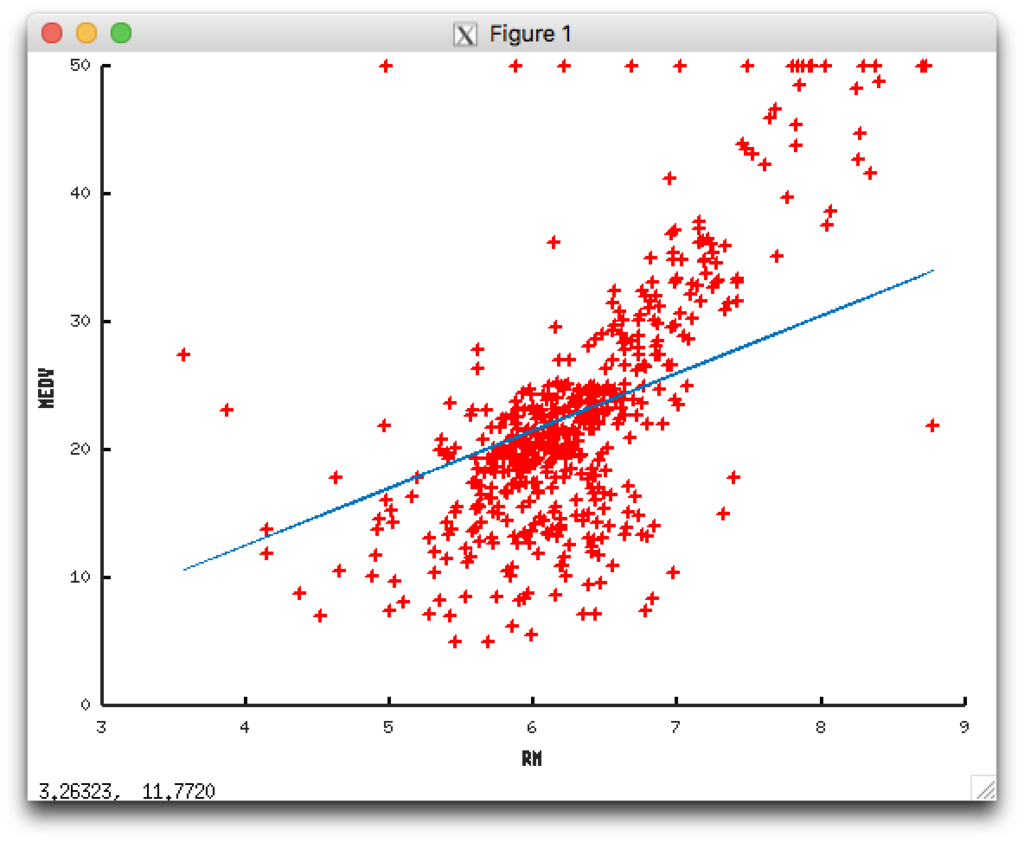
データにフィットした直線がプロットできたようです。

出力した数値

1
2
3
4
5

J =  296.07
initial cost 296.073458
final cost 27.131052
Theta found by gradient descent: -5.254087 4.477681
for RM = 5, MEDV = 17.134317

部屋数が５つのときに 17.134317と予想できました。グラフにプロットされたデータとフィットされているようです。

まとめ